学习笔记:NSGA-II算法
NSGA-II:基于 pareto 的改进非支配排序的遗传算法
进行多目标优化时,通常面临多个目标函数无法同时达到最优的情况,为了解决这一矛盾,引入Pareto-Optimality的概念
Pareto-Optimality
通常,多目标优化的一般形式为:
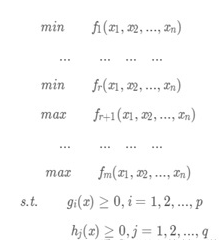
经过处理,可以化为以下形式:
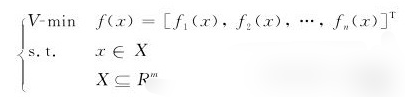
其中
f1(x),f2(x),…,fn(x)
为目标函数,其全部都是求最小值的形式
以下针对两个目标函数进行讨论:
有几个目标函数便为几维空间,有两个目标函数Time(f1(x)),Cost(f2(x)),
可以画出图像:
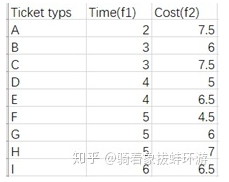
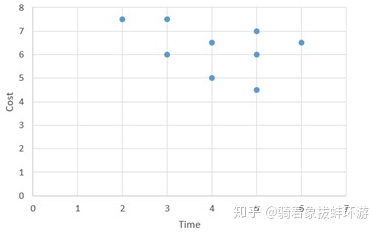
随后引入几个概念:
非支配解:假设任何二解S1 及S2 对所有目标而言,S1均优于S2,则我们称S1 支配S2,若S1 的解没有被其他解所支配,则S1 称为非支配解(不受支配解),也称Pareto解
支配解:若解S2的所有目标均劣于S1,则称S1优于S2,也称S1支配S2
,S2为受支配解。
因此现在的首要任务是寻找解空间里面所有的Pareto解,找到所有Pareto解之后,这些解组成的平面叫做Pareto前沿面(Non-dominated front)。在目标函数较多时,前沿面通常为超曲面。
非支配解排序(Non-dominated Sorting)
设所有解的集合为S,现从中找出非支配解集合,记为F1
令S=S-F1,从S中再找出非支配解集合,记为F2
重复第二步,直到S为空集
将每次找出的非支配解进行排序如下:
{F1,F2,…,Fn}
在途中画出Fi集合中对应点,并连线,则构成了n个pareto曲面,分别编号为Non-dominated Front 1,Non-dominated Front 2…
以上述表格中数据为例:F1={A,B,D,F}, F2={C,E,D}, F3={H,I}
画出相应图形:
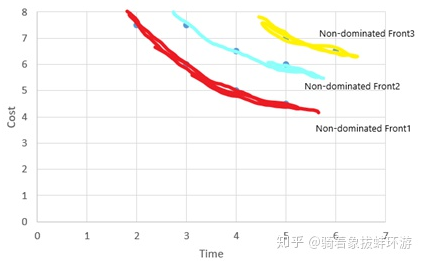
在第一个前沿面上的解具有最大的适应度,序数越大则适应度越小。序号小的前沿面上的解可以支配序号大的前沿面上的解。
同一前沿面上解的排序-拥挤度(Crowding Distances)
针对第一个前沿面来说,其中包含了A,B,D,F四个解,如何评判这四个解的适应度大小呢?由此引入了拥挤度的概念。
拥挤度的计算:
只考虑同一前沿面上的解,设定位于前沿面两端边界点的拥挤度为∞。
对于不在两端的点,其拥挤度主要与其相邻两个点有关
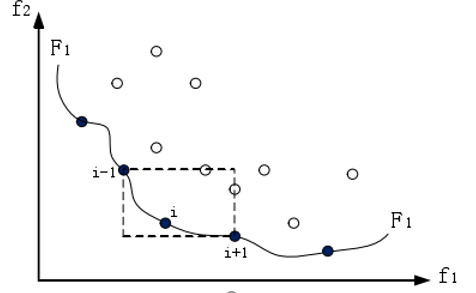
解i 的拥挤距离等于它在同一级相邻的两个解 i-1 与 i+1 总成的矩形的边长之和。
拥挤度越小则对应该解越重要
比较通俗的理解:拥挤度越小就说明该解与其他解相似程度不高,保留拥挤度较小的点相当于保存了解的多样性
所以说,确定解的适应度大小顺序应该先判断该解在哪个前沿面上,如果在同一个前沿面上,则再计算拥挤度进行判断
与遗传算法结合
与普通遗传算法步骤大概相同,初始化随机取几个解,进行编码,交叉互换,突变生成子代
但是,在生成子代后,需要与父代混合,从中挑选出适应度较高的解重新形成子代,再进行新的一轮迭代。
举例说明:
1.针对一个两目标优化问题,初始化随机取出10个解记为F,经过计算得到子一代为P
此时将P,F混合,形成新的解集S
2.针对S,进行上面所介绍的非支配解排序,计算拥挤度,最终得出这12个解的适应度大小顺序,从中取适应度较大的10个点生成新的子代(维持和父代个数相同),带入算法进行新一轮迭代
子代父代混合筛选生成新的子代,好像叫做精英策略
任何启发式算法均有两个方面组成:加快收敛的操作和在收敛过程中保持解的多样性的操作,两种操作相互作用,以至于找到一个合适的收敛速度,减少计算时间,同时避免陷入局部最优
对于NSGA来说,其规则仍然符合这两个准则:
本算法并不是只取最优的前沿面,而是将所有前沿面均纳入考虑范围内,是为了体现解的多样性,防止陷入局部最优
计算拥挤度是为了保存下来相似程度较低的解,保持解空间的多样性
使用精英策略是为了加速收敛,更快的除去劣解
以上内容转载自 知乎文章 NSGA2 遗传算法解决多目标优化 作者:骑着象拔蚌环游













